Ex 5: Time-varying natural mortality linked to the Gulf Stream Index • wham

In this vignette we walk through an example using the wham (WHAM = Woods Hole Assessment Model) package to run a state-space age-structured stock assessment model. WHAM is a generalization of code written for Miller et al. (2016) and Xu et al. (2018), and in this example we apply WHAM to the same stock, Southern New England / Mid-Atlantic Yellowtail Flounder.

This is the 5th WHAM example, which builds off example 2 (also available as an R script :

full state-space model (numbers-at-age are random effects for all ages, NAA_re = list(sigma='rec+1',cor='iid'))
logistic normal age compositions, pooling zero observations with adjacent ages (age_comp = "logistic-normal-pool0")
random-about-mean recruitment (recruit_model = 2)
5 indices
fit to 1973-2011 data

We assume you already have wham installed. If not, see the Introduction. The simpler 1st example, without environmental effects or time-varying $M$, is available as a R script and vignette.

In example 5, we demonstrate how to specify and run WHAM with the following options for natural mortality:

not estimated (fixed at input values)
one value, $M$
age-specific, $M_a$ (independent)
function of weight-at-age, $M_{y,a} = \mu_M * W_{y,a}^b$
AR1 deviations by age (random effects), $M_{y,a} = \mu_M + \delta_a \quad\mathrm{and}\quad \delta_a \sim \mathcal{N} (\rho_a \delta_{a-1}, \sigma^2_M)$
AR1 deviations by year (random effects), $M_{y,a} = \mu_M + \delta_y \quad\mathrm{and}\quad \delta_y \sim \mathcal{N} (\rho_y \delta_{y-1}, \sigma^2_M)$
2D AR1 deviations by age and year (random effects), $M_{y,a} = M_a + \delta_{y,a} \quad\mathrm{and}\quad \delta_{y,a} \sim \mathcal{N}(0,\Sigma)$

We also demonstrate alternate specifications for the link between $M$ and an environmental covariate, the Gulf Stream Index (GSI), as in O’Leary et al. (2019):

none
linear (in log-space), $M_{y,a} = e^{\mathrm{log}\mu_M + \beta_1 E_y}$
quadratic (in log-space), $M_{y,a} = e^{\mathrm{log}\mu_M + \beta_1 E_y + \beta_2 E^2_y}$

Note that you can specify more than one of the above effects on $M$, although the model may not be estimable. For example, the most complex model with weight-at-age, 2D AR1 age- and year-deviations, and a quadratic environmental effect: $M_{y,a} = e^{\mathrm{log}\mu_M + b W_{y,a} + \beta_1 E_y + \beta_2 E^2_y + \delta_{y,a}}$.

1. Load data

Open R and load wham and other useful packages:

library(wham)
library(ggplot2)
library(tidyr)
library(dplyr)
library(viridis)

For a clean, runnable .R script, look at ex5_M_GSI.R in the example_scripts folder of the wham package. You can run this entire example script with:

wham.dir <- find.package("wham")
source(file.path(wham.dir, "example_scripts", "ex5_M_GSI.R"))

Let’s create a directory for this analysis:

# choose a location to save output, otherwise will be saved in working directory
write.dir <- "choose/where/to/save/output" # need to change e.g., tempdir(check=TRUE)
dir.create(write.dir)
setwd(write.dir)

We need the same ASAP data file as in example 2, and the environmental covariate (Gulf Stream Index, GSI). Read in ex2_SNEMAYT.dat and GSI.csv:

asap3 <- read_asap3_dat(file.path(wham.dir,"extdata","ex2_SNEMAYT.dat"))
env.dat <- read.csv(file.path(wham.dir,"extdata","GSI.csv"), header=T)
head(env.dat)

The GSI does not have a standard error estimate, either for each yearly observation or one overall value. In such a case, WHAM can estimate the observation error for the environmental covariate, either as one overall value, $\sigma_E$, or yearly values as random effects, $\mathrm{log}\sigma_{E_y} \sim \mathcal{N}(\mathrm{log}\sigma_E, \sigma^2_{\sigma_E})$. In this example we choose the simpler option and estimate one observation error parameter, shared across years.

2. Specify models

Now we specify 14 models with different options for natural mortality:

Ecov_how <- paste0(
  c("none",rep("",2), rep("none", 9), rep("", 2)),
  c("", rep("lag-0-",2), rep("",9), rep("lag-0-",2)),
  c("", "linear", "poly-2", rep("",9), "linear", "poly-2"))

mean_model <- c(rep("fixed-M",6), "estimate-M", "weight-at-age", rep("estimate-M",6))
age_specific <- c(rep(NA,6),TRUE, NA, rep(FALSE, 6))

df.mods <- data.frame(M_model = c(rep("---",6),"age-specific","weight-at-age",rep("constant",6)),
                      mean_model = mean_model,
                      age_specific = age_specific,
                      M_re = c(rep("none",3),"ar1_a","ar1_y","ar1_ay",rep("none",3),"ar1_a", "ar1_y",rep("ar1_ay",3)),
                      Ecov_process = rep("ar1",14),
                      Ecov_how = Ecov_how, stringsAsFactors=FALSE)
n.mods <- dim(df.mods)[1]
df.mods$Model <- paste0("m",1:n.mods)
df.mods <- df.mods %>% select(Model, everything()) # moves Model to first col

Look at the model table:

df.mods
#>    Model       M_model    mean_model age_specific   M_re Ecov_process
#> 1     m1           ---       fixed-M           NA   none          ar1
#> 2     m2           ---       fixed-M           NA   none          ar1
#> 3     m3           ---       fixed-M           NA   none          ar1
#> 4     m4           ---       fixed-M           NA  ar1_a          ar1
#> 5     m5           ---       fixed-M           NA  ar1_y          ar1
#> 6     m6           ---       fixed-M           NA ar1_ay          ar1
#> 7     m7  age-specific    estimate-M         TRUE   none          ar1
#> 8     m8 weight-at-age weight-at-age           NA   none          ar1
#> 9     m9      constant    estimate-M        FALSE   none          ar1
#> 10   m10      constant    estimate-M        FALSE  ar1_a          ar1
#> 11   m11      constant    estimate-M        FALSE  ar1_y          ar1
#> 12   m12      constant    estimate-M        FALSE ar1_ay          ar1
#> 13   m13      constant    estimate-M        FALSE ar1_ay          ar1
#> 14   m14      constant    estimate-M        FALSE ar1_ay          ar1
#>        Ecov_how
#> 1          none
#> 2  lag-0-linear
#> 3  lag-0-poly-2
#> 4          none
#> 5          none
#> 6          none
#> 7          none
#> 8          none
#> 9          none
#> 10         none
#> 11         none
#> 12         none
#> 13 lag-0-linear
#> 14 lag-0-poly-2

The first 6 models fix mean natural mortality rates. Some of these models assume age and or year varying random effects or effects of GSI on M. Model 7 estimates age-specific M as fixed effects and Model 8 estimates M as a function of weight at age. Models 9-14 make similar assumptions to models 1-6, but a constant mean M parameter (across age and time) is estimated.

3. Natural mortality options

We specify the options for modeling natural mortality by including an optional list argument, M, to the prepare_wham_input() function (see the prepare_wham_input() and set_M() help pages). M specifies estimation options and can overwrite M-at-age values specified in the ASAP data file. By default (i.e. M is NULL or not included), the M-at-age matrix from the ASAP data file is used (M fixed, not estimated). M is a list that includes following entries relevant here:

$mean_model: Natural mortality model options.
- "constant": estimate a single $M$, shared across all ages and years.
- "age-specific": estimate $M_a$ independent for each age, shared across years.
- "weight-at-age": estimate $M$ as a function of weight-at-age, $M_{y,a} = \mu_M * W_{y,a}^b$, as in Lorenzen (1996) and Miller & Hyun (2018).
$re_model: Time- and age-varying random effects on $M$.
- "none": $M$ constant in time and across ages (default).
- "iid_a": $M$ varies by age, but uncorrelated and constant over years.
- "iid_y": $M$ varies by year, but uncorrelated and constant over age.
- "iid_ay": $M$ varies by year and age, but uncorrelated.
- "ar1_a": $M$ correlated by age (AR1), constant in time.
- "ar1_y": $M$ correlated by year (AR1), constant by age.
- "ar1_ay": $M$ correlated by year and age (2D AR1), as in Cadigan (2016).
$initial_means: an array of initial/mean M parameters (n_stocks x n_regions x n_ages). If NULL, initial mean M-at-age values are taken from the first row of the MAA matrix in the ASAP data file(s).
$means_map: an array of integers (n_stocks x n_regions x n_ages) of that distinguishes which mean parameters to estimate and whether any should have the same value. In all models we have 1 stock and 1 region and 6 ages. So to estimate different M for each age we set: $means_map = array(1:6, dim = c(1,1,6)). If NULL, $M$ at all ages is fixed at M$initial_means (if not NULL) or row 1 of the MAA matrix from the ASAP file(s) (if M$initial_means = NULL).

For example, to fit model m1, fix $M_a$ at values in ASAP file:

M <- NULL # or simply leave out of call to prepare_wham_input

To fit model m9, estimate one $M$, constant by year and age:

M <- list(mean_model="estimate-M", means_map = array(1,dim = c(1,1,6)))

To fit model m12 where we estimate a mean $M$ parameter and 2DAR1 deviations by year and age:

M <- list(model="estimate-M", means_map = array(1, dim = c(1,1,asap3[[1]]$dat$n_ages)), re_model="ar1_ay")

To fit model m11, use the $M_a$ values specified in the ASAP file, but with 2D AR1 deviations as in Cadigan (2016):

M <- list(re_model=matrix("ar1_ay",1,1))

4. Linking M to an environmental covariate (GSI)

As described in example 2, the environmental covariate options are fed to prepare_wham_input() as a list, ecov. This example differs from example 2 in that:

We will estimate the observation error for the GSI (one overall value for all years): $logsigma = "est_1". The other option is "est_re" to allow the GSI observation error to have yearly fluctuations (random effects). The Cold Pool Index in example 2 had yearly observation errors given.
We will assume GSI affects $M$ rather than recruitment.
We will assume a lag of 0 for the effect of GSI on $M$: GSI in year t affects $M$ in year t, instead of year t+1.
We will consider models with and without the effect of GSI on $M$, but keep the state-space model for GSI in the model to allow AIC comparisons.
We will consider both linear and quadratic effects of GSI on $M$. WHAM includes a function to calculate orthogonal polynomials in TMB, akin to the poly() function in R.

For example, the ecov list for model m3 with a quadratic GSI-M effect:

  # example for model m3
  ecov <- list(
    label = "GSI",
    mean = as.matrix(env.dat$GSI),
    logsigma = 'est_1', # estimate obs sigma, 1 value shared across years
    year = env.dat$year,
    use_obs = matrix(1, ncol=1, nrow=dim(env.dat)[1]), # use all obs (=1)
    lag = 0, # GSI in year t affects M in same year
    process_model = "ar1", # GSI modeled as AR1 (random walk would be "rw")
    M_how = array("lag-0-poly-2",c(1,1,6,1))) # n_Ecov x n_stocks x n_ages x n_regions

Note that you can set ecov = NULL to fit the model without environmental covariate data, but here we fit the ecov data even for models without GSI effect on $M$ (m1, m4-12) so that we can compare them via AIC (need to have the same data in the likelihood). We accomplish this by setting ecov$M_how = array("none",c(1,1,6,1)) and ecov$process_model = "ar1".

5. Run all models

All models use the same options for recruitment (random-about-mean, no stock-recruit function) and selectivity (logistic, with parameters fixed for indices 4 and 5).

mods <- list()
for(m in 1:n.mods){
  ecov <- list(
    label = "GSI",
    mean = as.matrix(env.dat$GSI),
    logsigma = 'est_1', # estimate obs sigma, 1 value shared across years
    year = env.dat$year,
    use_obs = matrix(1, ncol=1, nrow=dim(env.dat)[1]), # use all obs (=1)
    process_model = df.mods$Ecov_process[m], # "rw" or "ar1"
    M_how = array(df.mods$Ecov_how[m],c(1,1,asap3[[1]]$dat$n_ages,1))) # n_Ecov x n_stocks x n_ages x n_regions

  mean_map <- NULL
  if(df.mods$mean_model[m] == "estimate-M"){
    if(df.mods$age_specific[m]) mean_map[1,1,] <- 1:asap3[[1]]$dat$n_ages
    else mean_map[1,1,] <- 1
  }
  M <- list(
    mean_model = df.mods$mean_model[m],
    re_model = matrix(df.mods$M_re[m], 1,1),
    means_map = mean_map
  )
  if(df.mods$mean_model[m] == "estimate-M" & !df.mods$age_specific[m]) M$initial_means = array(0.28, c(1,1,asap3[[1]]$dat$n_ages)) #n_stocks x n_regions x n_ages

  input <- prepare_wham_input(asap3, recruit_model = 2,
    model_name = paste0("m",m,": ", df.mods$mean_model[m]," + GSI link: ",df.mods$Ecov_how[m]," + M RE: ", df.mods$M_re[m]),
    ecov = ecov,
    selectivity=list(model=rep("logistic",6),
      initial_pars=c(rep(list(c(3,3)),4), list(c(1.5,0.1), c(1.5,0.1))),
      fix_pars=c(rep(list(NULL),4), list(1:2, 1:2))),
    NAA_re = list(sigma='rec+1',cor='iid'),
    M=M,
    age_comp = "logistic-normal-pool0")

  # Fit model
  mods[[m]] <- fit_wham(input, do.retro=T, do.osa=F) # turn off OSA residuals to save time

  # Save model
  saveRDS(mod[[m]], file=paste0(df.mods$Model[m],".rds"))

  # If desired, plot output in new subfolder
  # plot_wham_output(mod=mod, dir.main=file.path(getwd(),df.mods$Model[m]), out.type='html')
  
  # If desired, do projections
  # mod_proj <- project_wham(mod)
  # saveRDS(mod_proj, file=paste0(df.mods$Model[m],"_proj.rds"))
}

6. Compare models

Get model convergence and stats.

opt_conv = 1-sapply(mods, function(x) x$opt$convergence)
ok_sdrep = sapply(mods, function(x) if(x$na_sdrep==FALSE & !is.na(x$na_sdrep)) 1 else 0)
df.mods$conv <- as.logical(opt_conv)
df.mods$pdHess <- as.logical(ok_sdrep)

Only calculate AIC and Mohn’s rho for converged models.

df.mods$runtime <- sapply(mods, function(x) x$runtime)
df.mods$NLL <- sapply(mods, function(x) round(x$opt$objective,3))
is_conv <- df.mods$conv & df.mods$pdHess
which(is_conv) # 1, 2, 5, 8, 9, 11, 12
mods2 <- mods[is_conv]
#mods2[not_conv] <- NULL
df.aic.tmp <- as.data.frame(compare_wham_models(mods2, table.opts=list(sort=FALSE, calc.rho=TRUE))$tab)
df.aic <- df.aic.tmp[FALSE,]
ct = 1
for(i in 1:n.mods){
  if(!is_conv[i]){
    df.aic[i,] <- rep(NA,5)
  } else {
    df.aic[i,] <- df.aic.tmp[ct,]
    ct <- ct + 1
  }
}
df.aic[,1:2] <- format(round(df.aic[,1:2], 1), nsmall=1)
df.aic[,3:5] <- format(round(df.aic[,3:5], 3), nsmall=3)
df.aic[grep("NA",df.aic$dAIC),] <- "---"
df.mods <- cbind(df.mods, df.aic)
rownames(df.mods) <- NULL

Look at results table.

df.mods

7. Results

In the table, we have highlighted in gray models which converged and successfully inverted the Hessian to produce SE estimates for all (fixed effect) parameters. WHAM stores this information in mod$na_sdrep (should be FALSE), mod$sdrep$pdHess (should be TRUE), and mod$opt$convergence (should be 0). See stats::nlminb() and TMB::sdreport() for details.

Model m12 (estimate mean $M$ and 2D AR1 deviations by year and age, no GSI effect) had the lowest AIC among converged models and was overwhelmingly supported relative to the other models (bold in table below). The retrospective patterns in SSB and $F$ were also negligble compared to other models as measured by Mohn’s $\rho$.

Model	M mean model	M RE model	GSI model	GSI link	Converged	Pos def Hessian	Runtime (mi	)\| N	L\|dAI	\|AIC	\|$\rho_{R} </th> <th style="text-align:left;"> \|$_{SSB}	\|$_{}
m1	—	none	ar1	none	TRUE	TRUE	0.82	-813.858	37.1	-1489.7	0.259	0.117	-0.145
m2	—	none	ar1	lag-0-linear	TRUE	TRUE	0.70	-819.584	27.6	-1499.2	0.400	0.150	-0.164
m3	—	none	ar1	lag-0-poly-2	TRUE	FALSE	2.68	-820.307	—	—	—	—	—
m4	—	ar1_a	ar1	none	TRUE	FALSE	0.84	-828.322	—	—	—	—	—
m5	—	ar1_y	ar1	none	TRUE	TRUE	0.75	-821.393	26.0	-1500.8	0.704	0.128	-0.133
m6	—	ar1_ay	ar1	none	FALSE	FALSE	0.39	-813.968	—	—	—	—	—
m7	age-specific	none	ar1	none	TRUE	FALSE	0.78	-837.559	—	—	—	—	—
m8	weight-at-age	none	ar1	none	TRUE	TRUE	0.57	-825.020	18.8	-1508.0	0.725	0.140	-0.144
m9	constant	none	ar1	none	TRUE	TRUE	0.58	-825.015	16.8	-1510.0	0.544	0.129	-0.141
m10	constant	ar1_a	ar1	none	TRUE	FALSE	1.02	-829.109	—	—	—	—	—
m11	constant	ar1_y	ar1	none	TRUE	TRUE	0.74	-825.399	20.0	-1506.8	1.186	0.414	-0.298
m12	constant	ar1_ay	ar1	none	TRUE	TRUE	0.85	-836.408	0.0	-1526.8	0.312	0.006	-0.044
m13	constant	ar1_ay	ar1	lag-0-linear	FALSE	FALSE	0.54	-845.739	—	—	—	—	—
m14	constant	ar1_ay	ar1	lag-0-poly-2	FALSE	FALSE	2.06	-845.339	—	—	—	—	—

Estimated M

Models allowed to estimate mean $M$ increased $M$ (m7-m14) compared to the fixed values in models m1-m6 (more green/yellow than blue).
Models that estimated $M_a$ (m4, m7, m10) had highest $M_a$ for ages 4-5.
Models that estimated $M_y$ (m5 and m11) had higher $M_y$ in the early 1990s and early 2000s.
Models with GSI effects and random effects deviations in M did not converge.

Model m6 left $M_a$ fixed at the values from the ASAP data file (as in m1) and estimated 2D AR1 deviations around these mean $M_a$, but this model did not converge. This is how $M$ was modeled in Cadigan (2016). Model m8 that assumed M as a function of weight at age estimated essentially no effect so that M was constant and a negative log likelihood essentially the same as model m9 that made the simpler assumption of a constant M estimated. Below is a plot of $M$ by age (y-axis) and year (x-axis) for all models. Models with a positive definite Hessian are solid, and models with non-positive definite Hessian are pale.

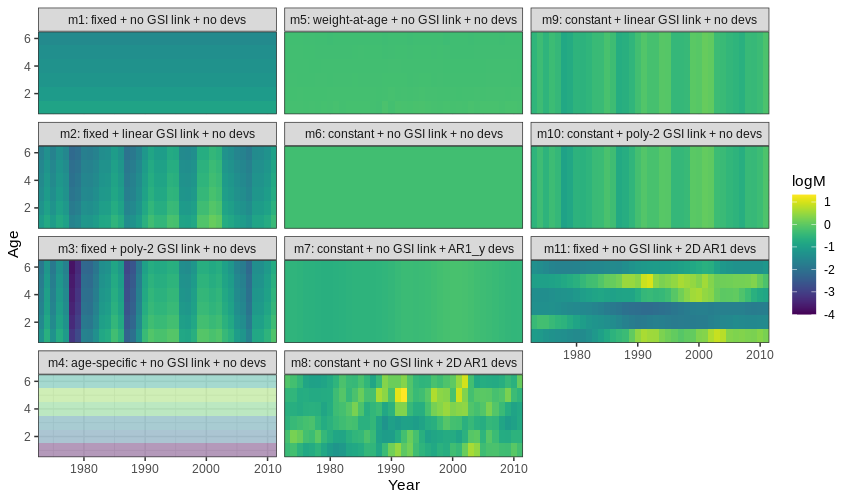
Natural mortality by age (y-axis) and year (x-axis) for all models.

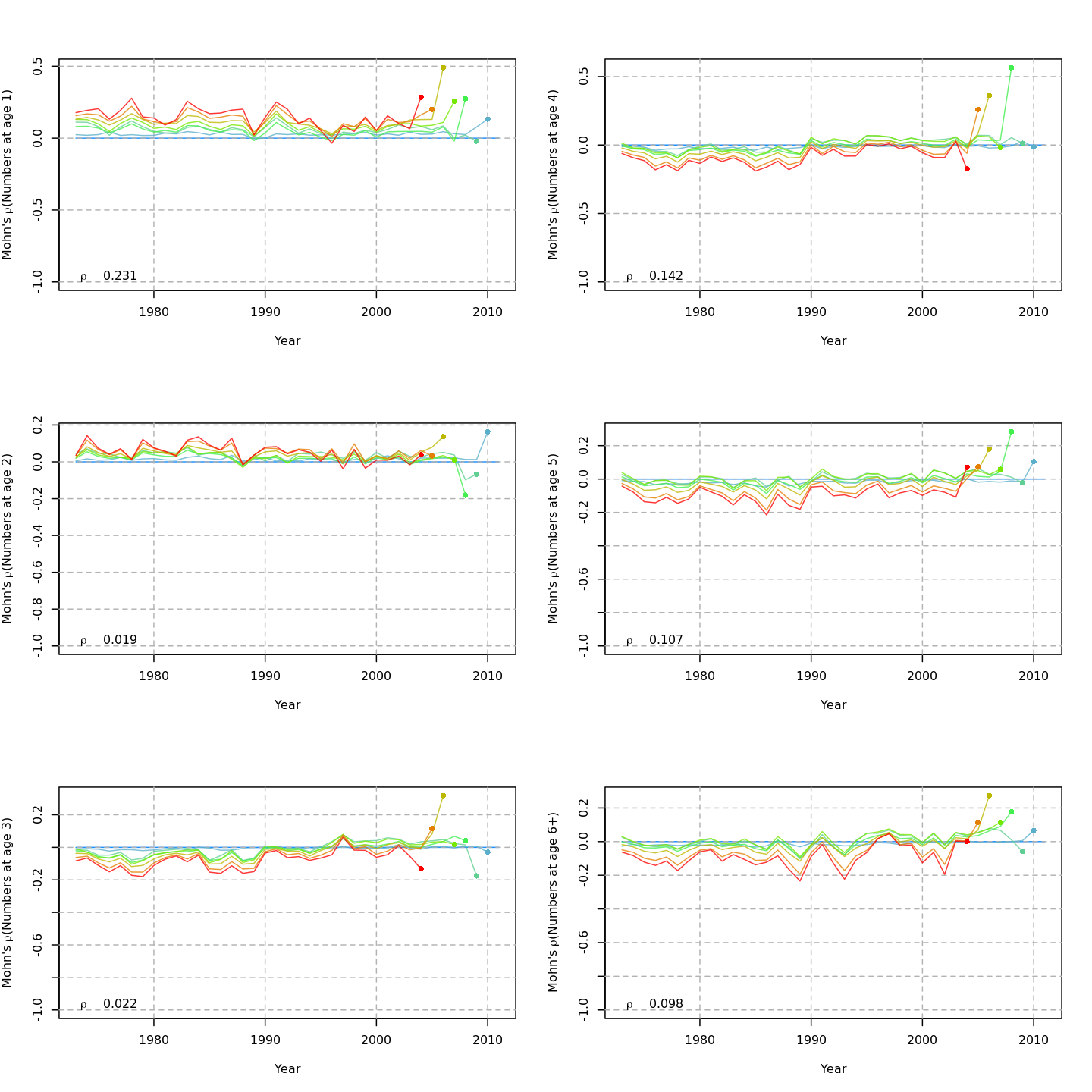
Retrospective patterns

Compared to m1, the retrospective pattern for m12 was slightly worse for recruitment (m12 0.31, m1 0.26) but improved for SSB (m8 0.01, m1 0.11) and F (m8 -0.04, m1 -0.15). Compare the retrospective patterns of numbers-at-age, SSB, and F for models m1 (left, fixed $M_a$) and m12 (right, estimated $M$ + 2D AR1 deviations).

Mohn’s rho for numbers-at-age, m1.

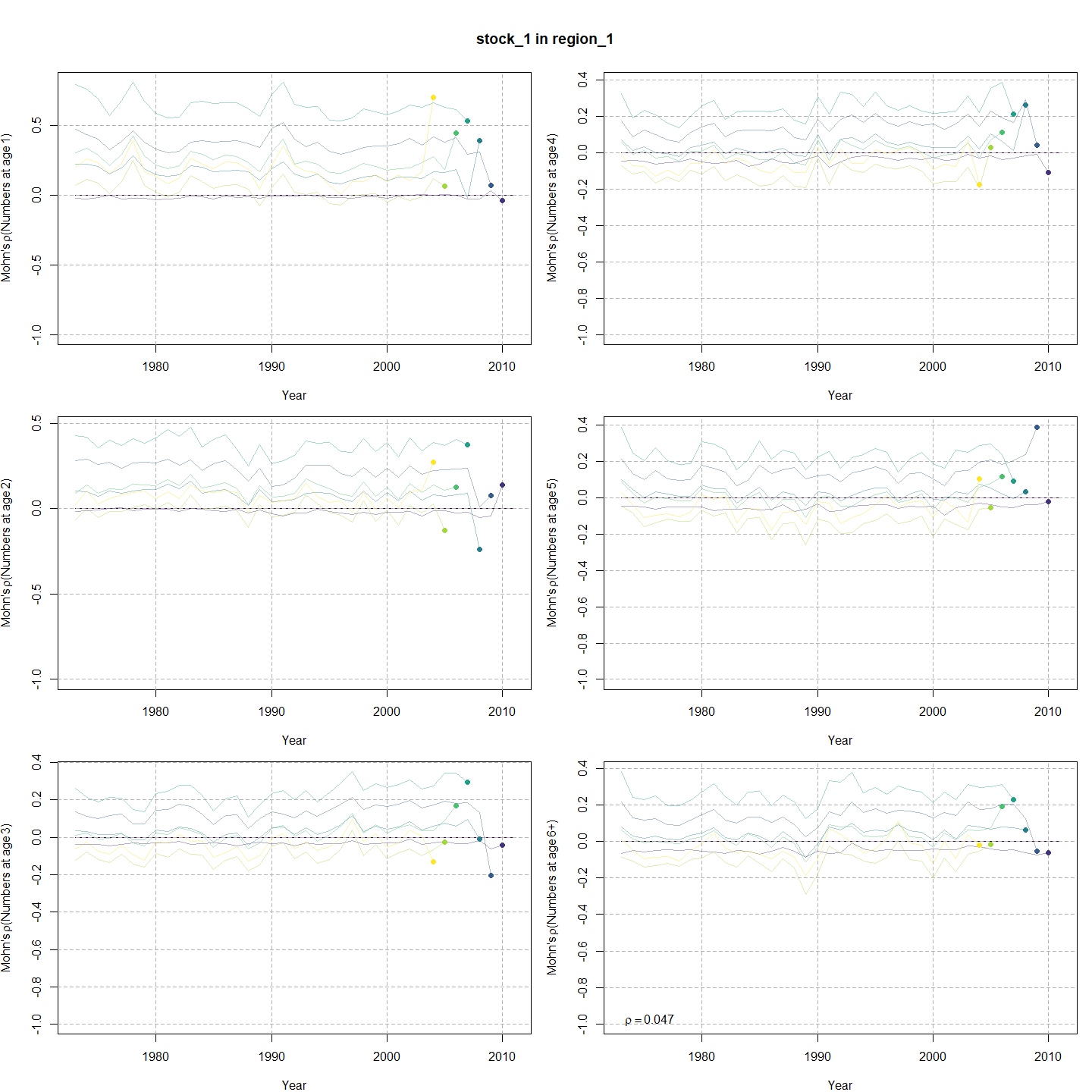
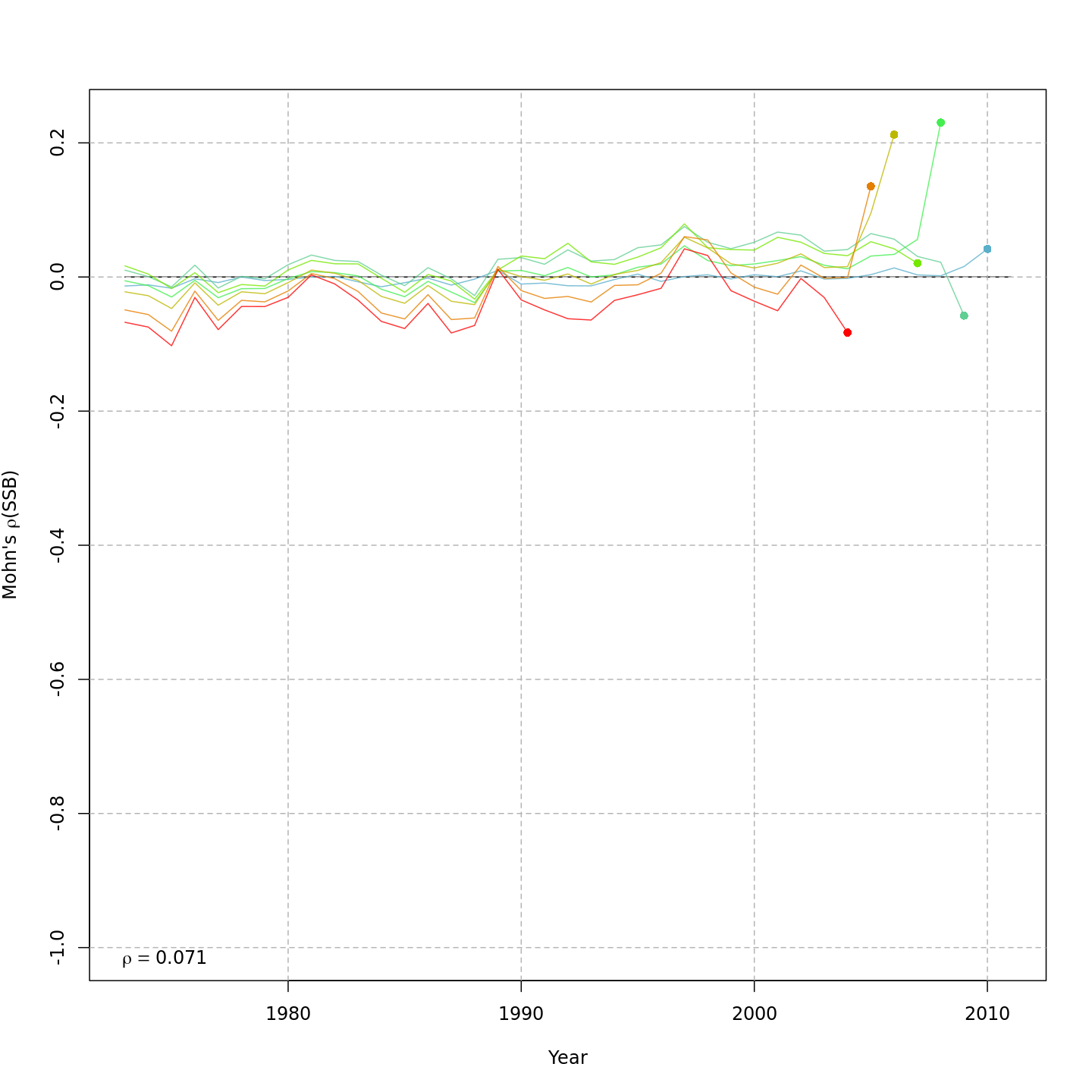
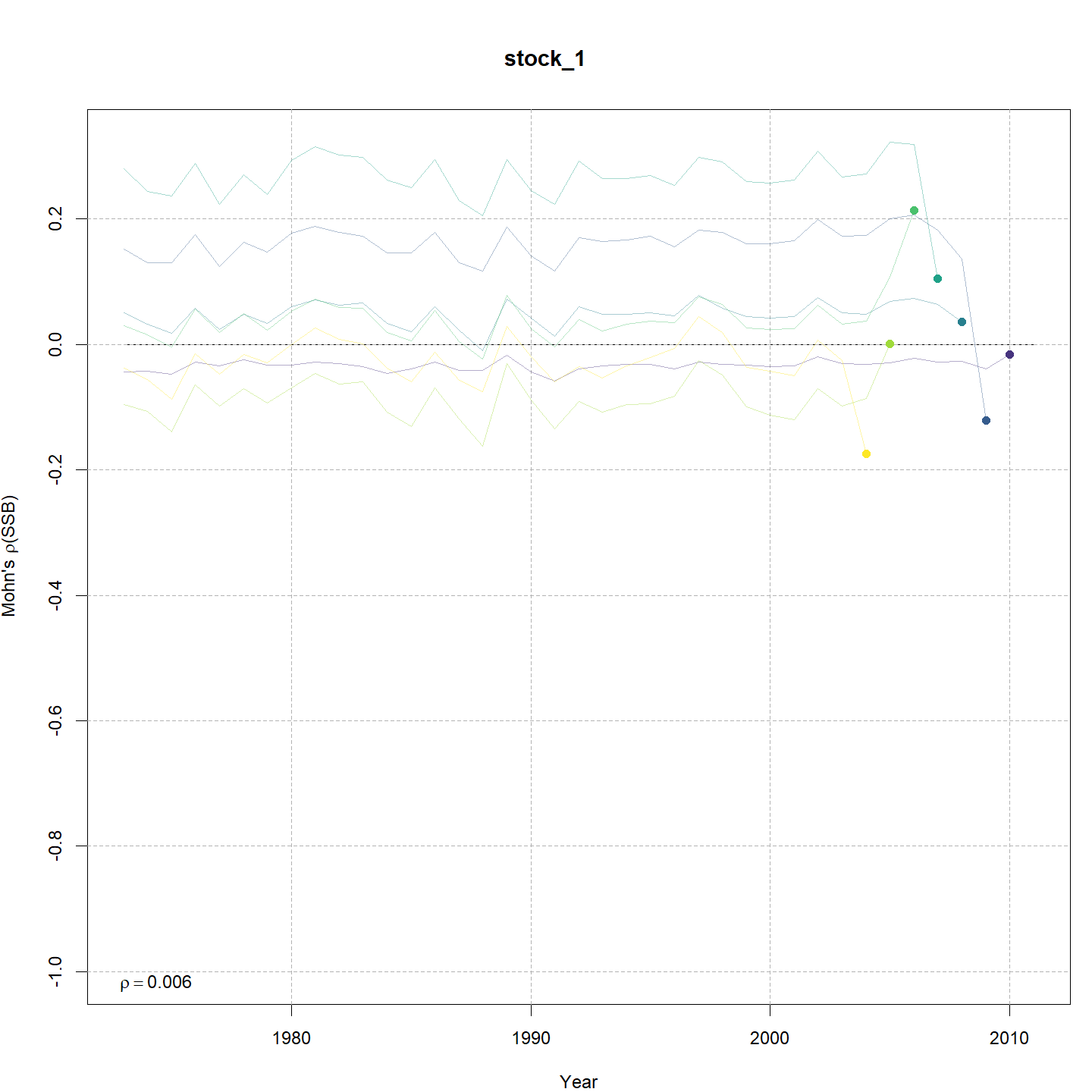
Mohn’s rho for SSB, m1. Mohn’s rho for SSB, m12.

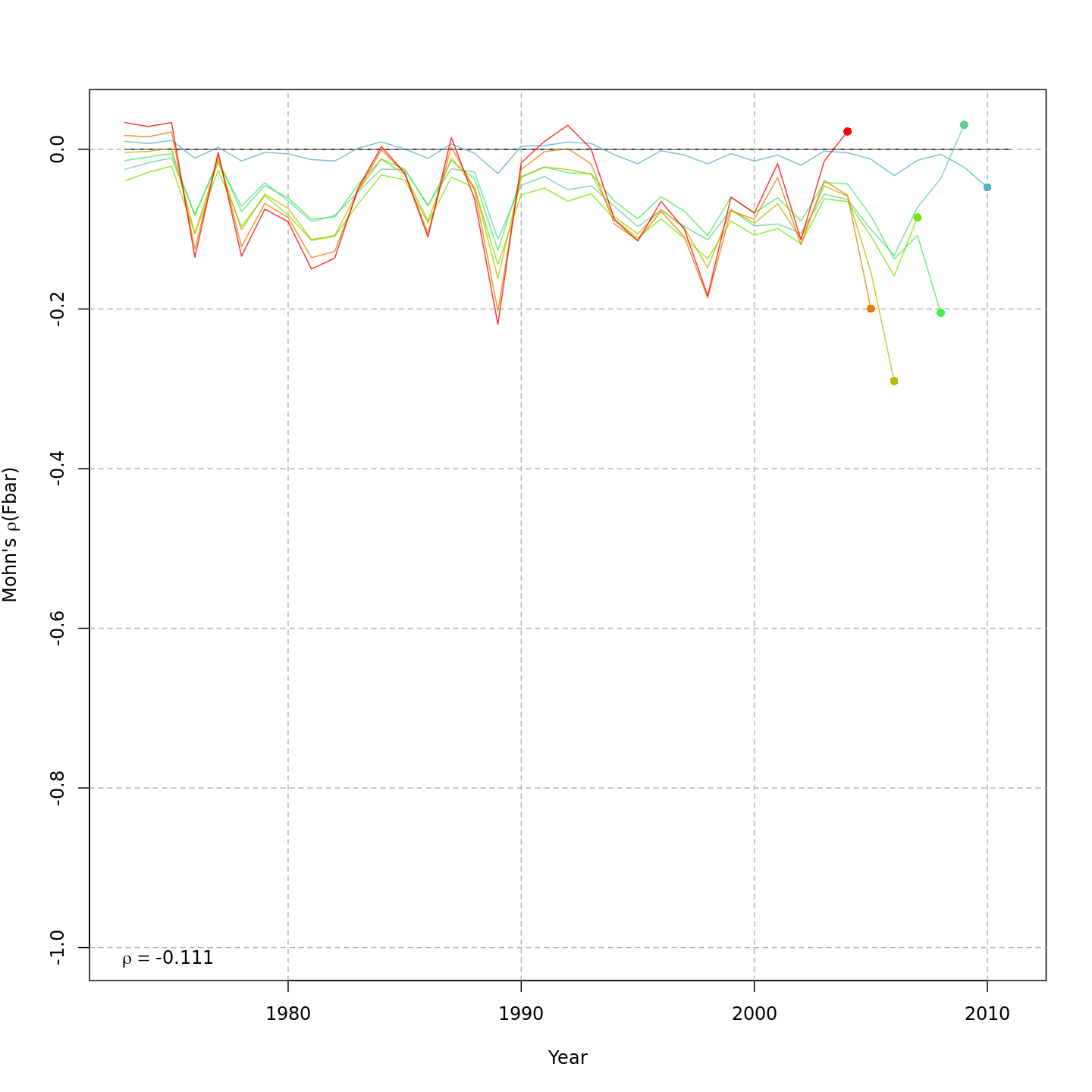
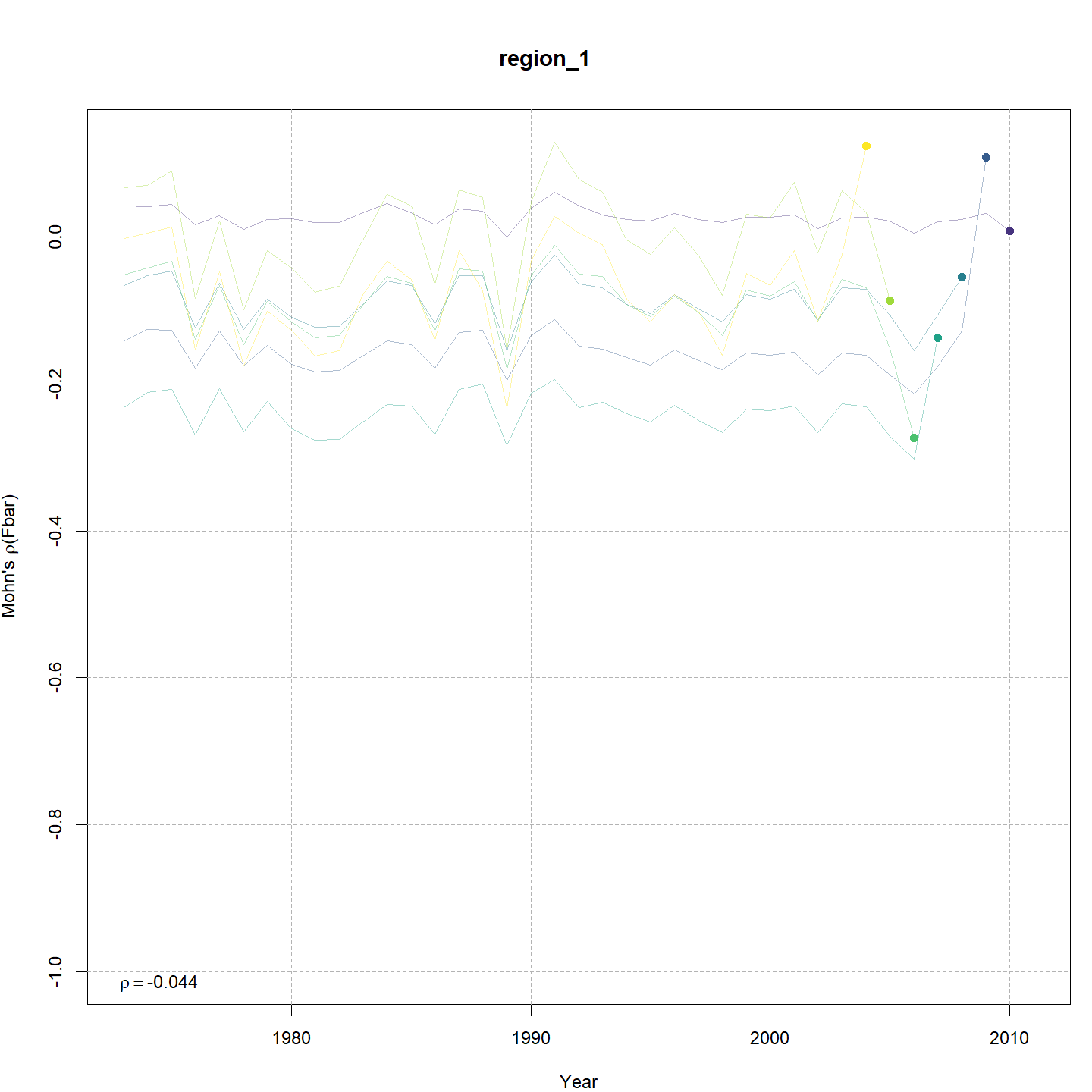
Mohn’s rho for F, m1. Mohn’s rho for F, m12.

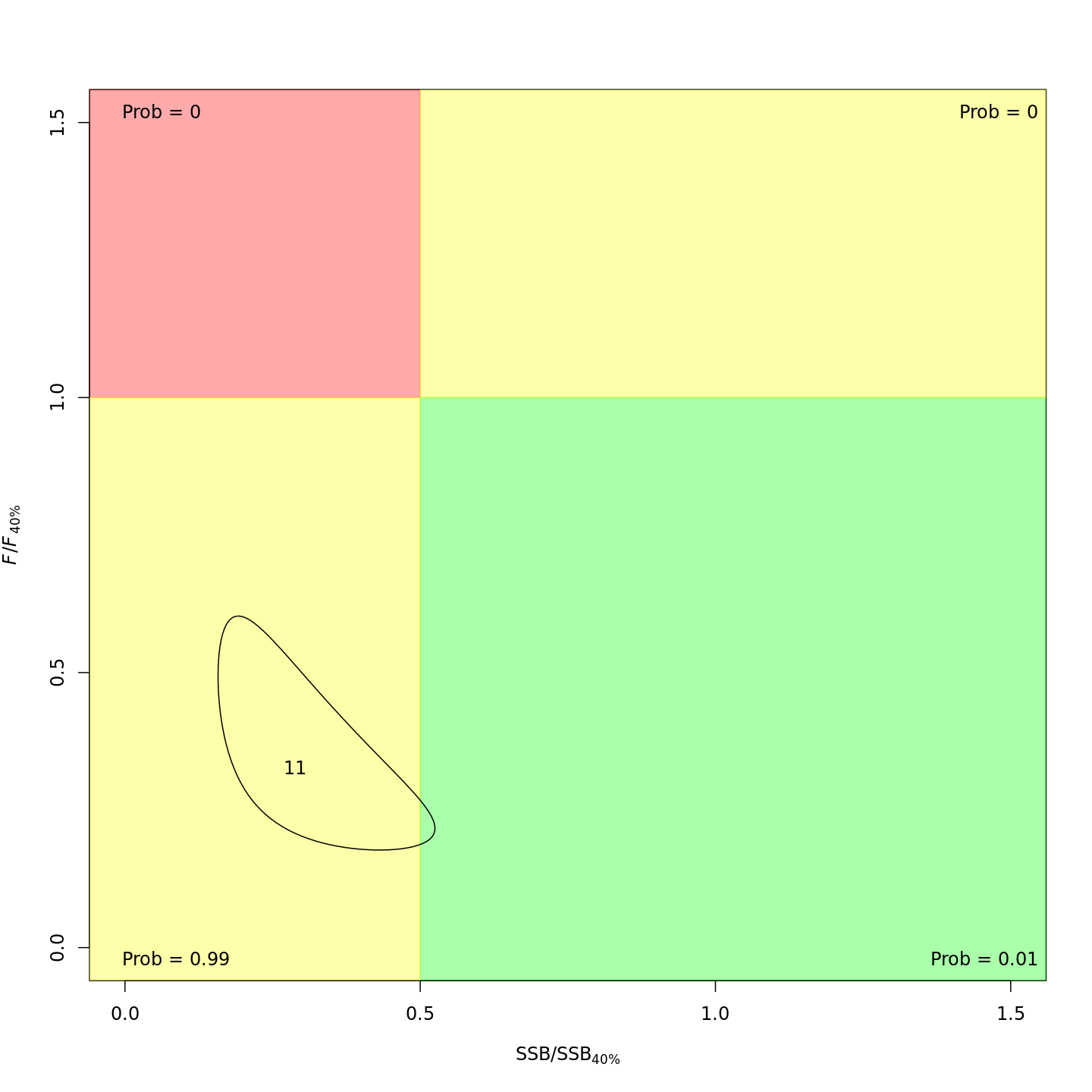
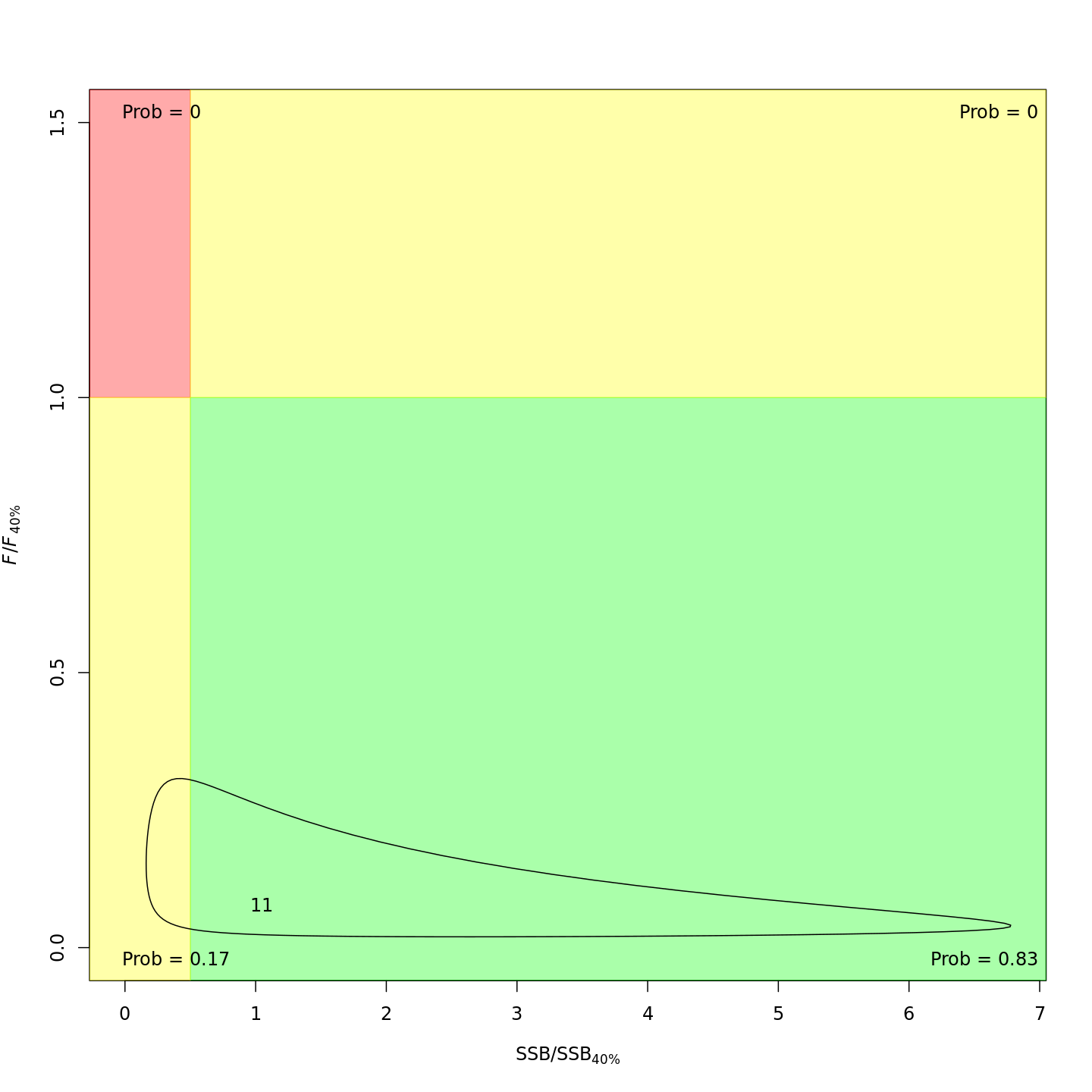
Stock status

Compared to m1 (left), m12 (right) estimated SPR-based reference points were more uncertain due to estimation of M rather than an assumed value. Model m12 estimates of $F_{40\%SPR}$ (middle) and yield at $F_{40\%SPR}$ (top) were higher, whereas estimates of SSB at $F_{40\%SPR}$ were generally lower.

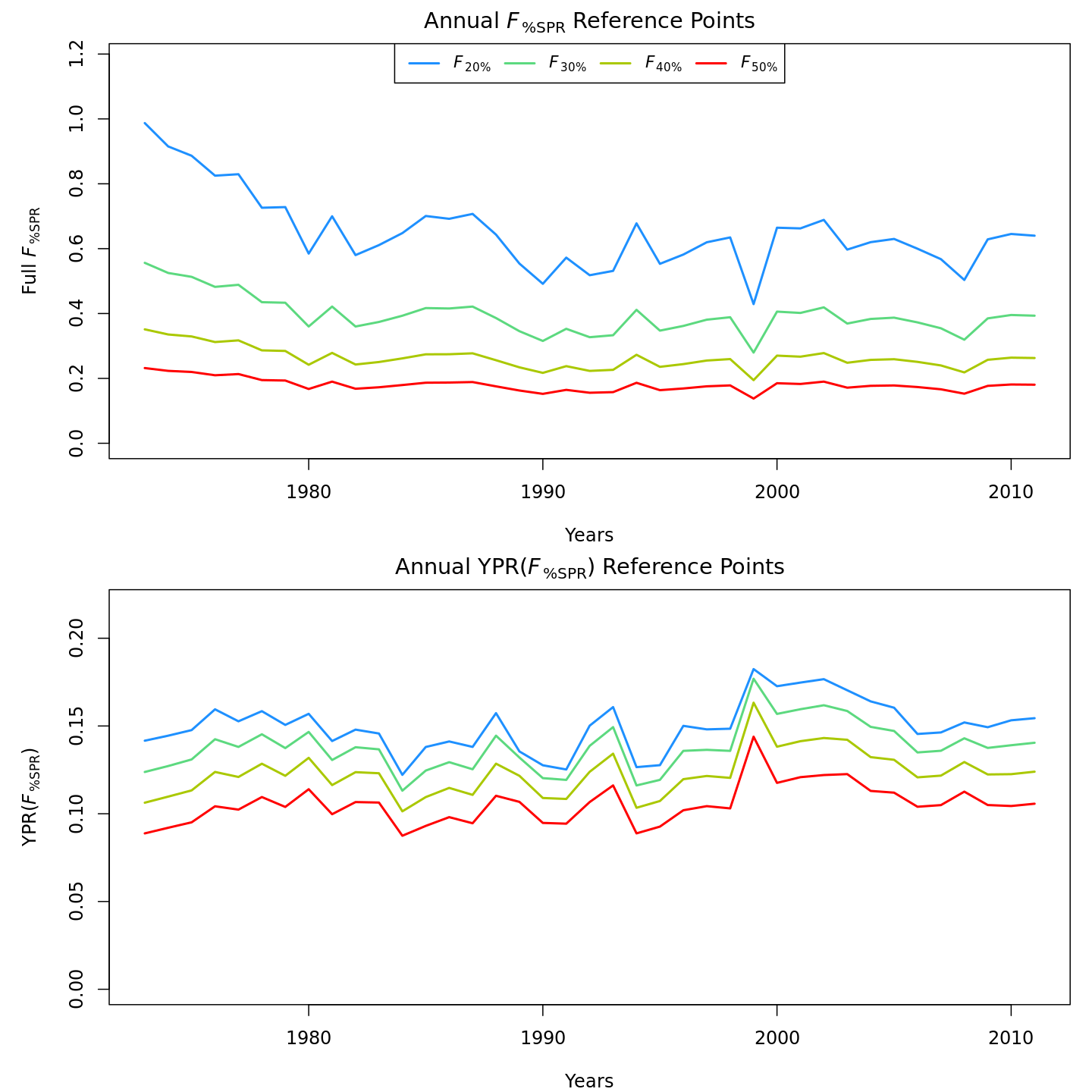
Reference point variability, m1.

Compared to m1 (left), m12 (right) estimated higher M and higher SSB – a much rosier picture of the stock status through time.

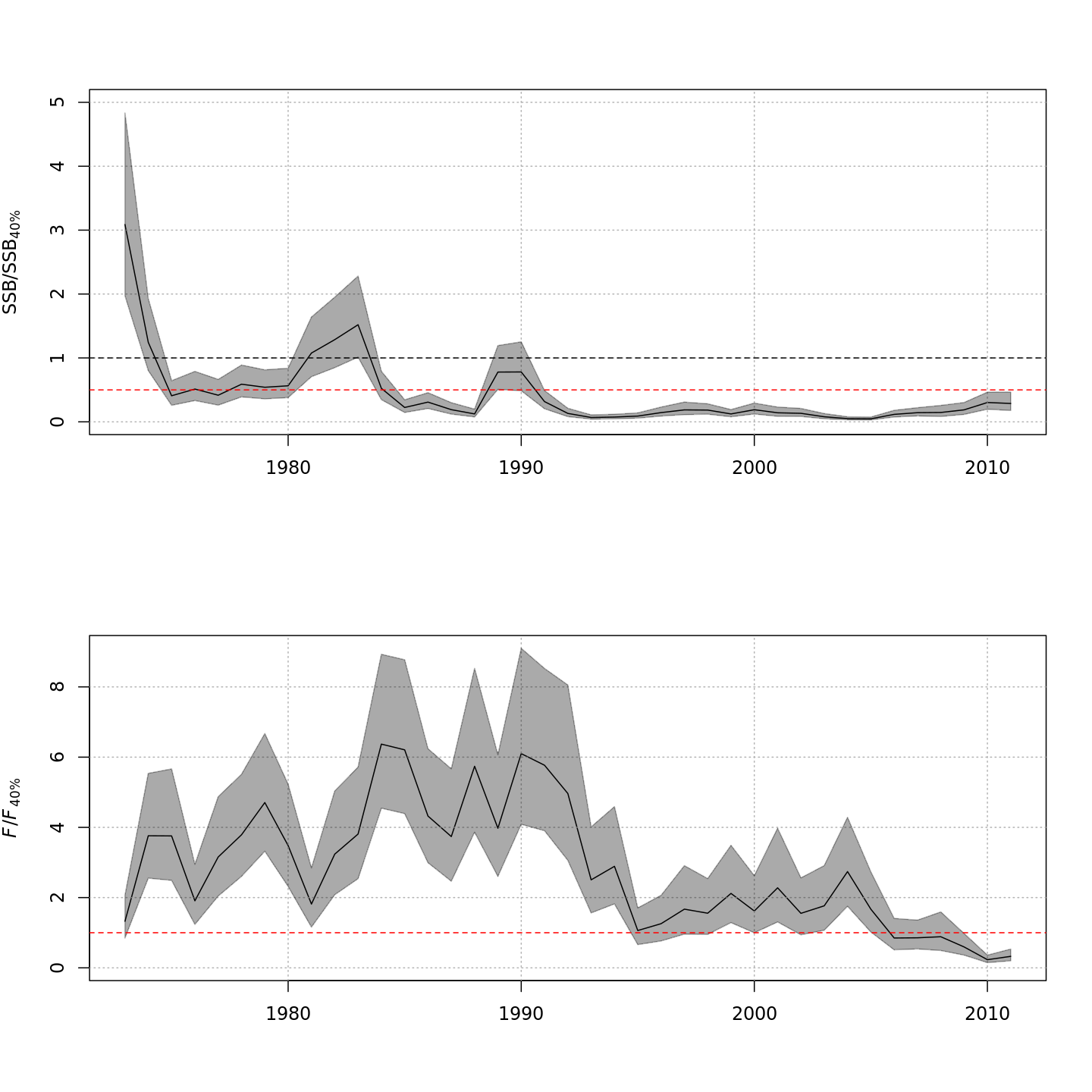
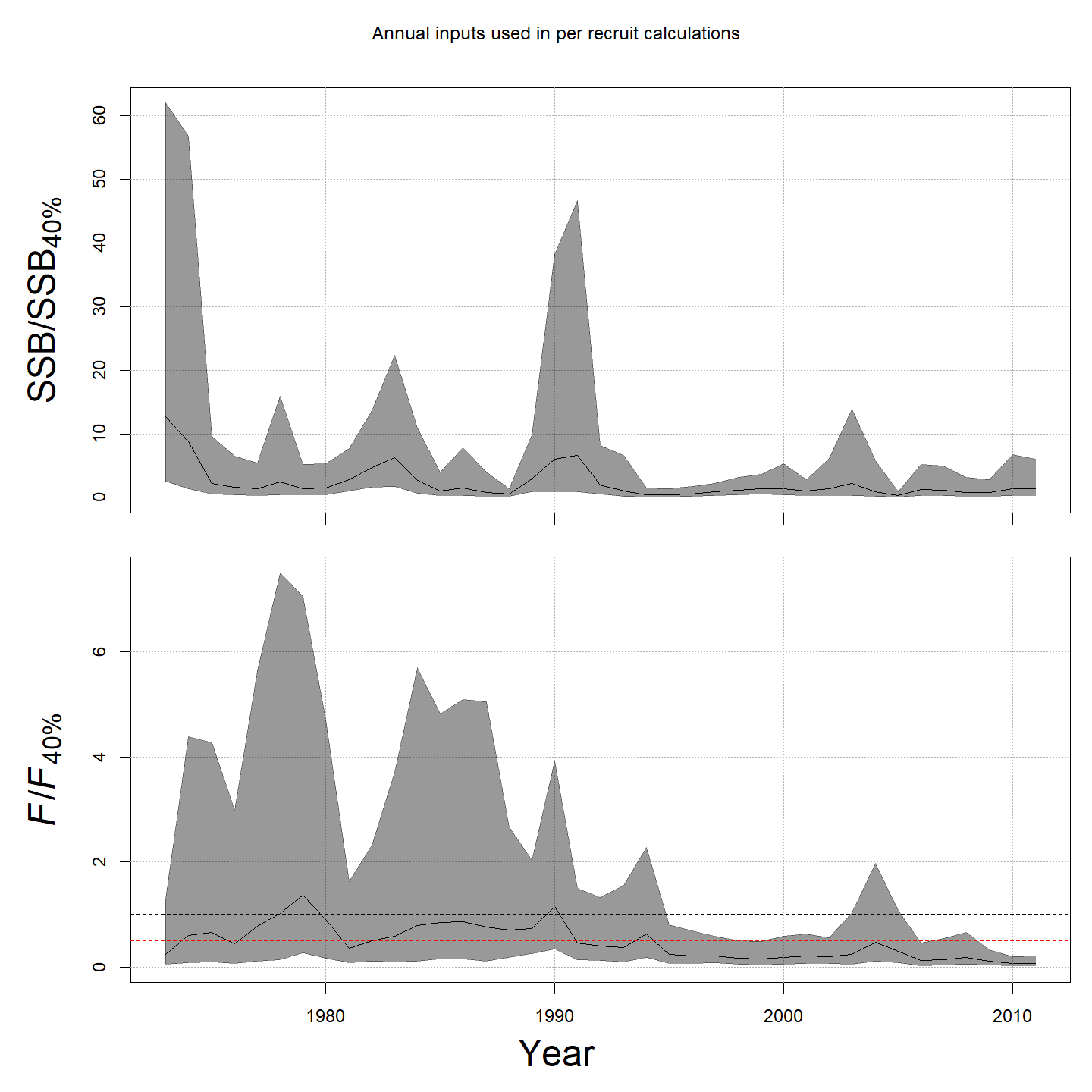
Relative stock status, m1. Relative stock status, m12.

In the final year (2011), m12 estimated much lower probabilities of the stock being overfished than m1 (1% vs. 93%).

Kobe status plot, m1. Kobe status plot, m12.

Yet more M options

If you want to estimate M-at-age shared/mirrored among some but not all ages, you can modify M$means_map.